In the context of this article, model complexity will mainly refer to how many parameters the model has (e.g. the number of hydraulic conductivity zones or pilot points), and not necessarily to the type of equations that the model is using (e.g. fully saturated vs Richards' equations, surface water as boundary conditions vs fully coupled sw-gw, etc.), which opens a broader discussion. Additionally, the existing observations have to be reasonably related to the predictive variables, in terms of type, locations, scales and associated stresses.
Figure 1: Relationship between model complexity and predictive uncertainty, taken from the Australian Groundwater Modelling Guidelines (Barnett et al, 2012).
Relationship between model complexity and predictive error
In simple terms, Figure 1 indicates that adding complexity to a model (e.g. adding K zones) allows us to obtain a better fit to the existing observations (e.g. a lower NRMS), which reduces predictive error/uncertainty, but that too much complexity (e.g. too many K zones) could potentially lead to overfitting and increased predictive error/uncertainty. It is concluded that a model should aim to have an optimal level of complexity. Clearly, the definition of the model parameters has to be related to the conceptual understanding of the system, to the available field information, and to the modelling objectives; however, for the purpose of this article we will just focus on the complexity of the model.
Example 1: Generic Excel model
We start with a very simple example implemented in Excel, to better understand the basic concepts behind Figure 1. The main idea is to (1) obtain synthetic observations from a generic model that will be known to us, (2) add a small error to each observation, (3) fit a series of trendlines with different degrees of complexity to the previously generated observations, and (4) compare the predictive capacity of each trendline with respect to the "true prediction" given by the model that was used to generate the synthetic observations.
It is clear that in real problems we will never know the "true prediction", which is the main reason why we model; it is only a convenient technique that allows us to illustrate the relationship between model complexity and predictive error. The generic model that we choose for creating the synthetic observations is f (x) = x ^ 2, with random errors between +/- 50, as shown in Figure 2.
Figure 2: Generic Excel model and synthetic observations including random error.
We fit trendlines with different degrees of complexity to our synthetic observations, starting with a line, moving forward with polynomials of degree 2, 4 and 6. For all trendlines we define a forecast period, which we visually compare to the "true prediction". The results are presented in Figure 3, which shows that:
increasing the model complexity always allows for a better fit to the existing observations (i.e. R2 gets closer to 1 as we increase the complexity),
increasing the complexity leads to better predictions up to a certain level of complexity,
increasing the complexity beyond that level affects the predictive capacity of the model due to overfitting.
This simple example shows that under- and over-parameterization can lead to significant predictive errors. It is also concluded that improving the fit as much as possible does not necessarily lead to better predictions; on the contrary, it can cause important predictive errors due to overfitting.
It is important to mention that if no errors would have been added to the synthetic observations, all adjusted polynomials would have led to a perfect fit (y = x ^ 2). This demonstrates that predictive error due to overfitting is an amplification of the measurement error, as indicated in Figure 1, confirming that the quality of the observations is fundamental for the modelling process.
Figure 3: Effect of model complexity on the predictive error for the generic Excel model.
Example 2: MODFLOW/MT3DMS model
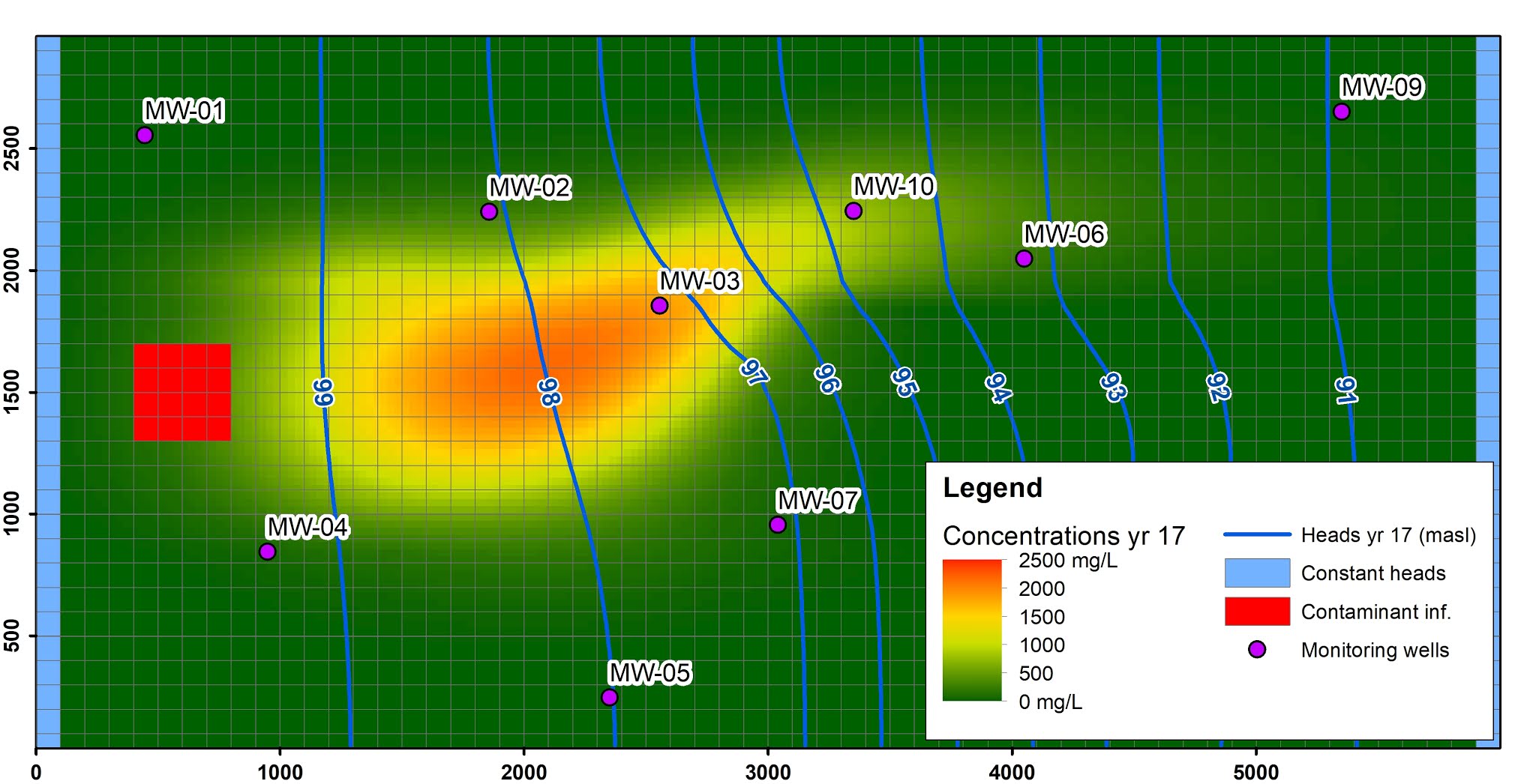
A flow and transport model is implemented using MODFLOW-2005 and MT3DMS to study the relationship between complexity and predictive error in groundwater models, with a brief description presented in Figure 4. The base model has twelve hydraulic conductivity zones, defining a known level of complexity. Infiltration of polluted water occurs over a period of 5 years with a concentration of 3000 mg/L, followed by a period of 45 years in which no infiltration occurs.
It is important to mention that the concepts explained in this article are also valid if pilot points instead of zones are being used, although additional considerations need to be taken. See the additional comments at the end of this article for more information.
Figure 4: Description of the MODFLOW/MT3DMS base model.
Similarly to the Excel model, synthetic observations are obtained from our base model (i.e. concentrations in MW-01 to MW-10), to which a certain amount of error is added. The objective is to use these observations to calibrate models with different degrees of complexity (i.e. the base model with different amount of K zones: 1, 6, 12, 36), and to visually compare the predictive capacity of each calibrated model with respect to the "true prediction" given by the base model. The results are presented in Figure 5, which corroborate the conclusions from the Excel model:
increasing the model complexity always allows for a better fit to the existing observations (i.e. adding K zones allows to obtain lower RMS values, with a particularly poor behaviour for the "1 zone model"),
increasing the complexity leads to better predictions up to a certain level of complexity,
increasing the complexity beyond that level affects the predictive capacity of the model due to overfitting.
It is important to understand that each calibrated model in Figure 5 corresponds to the highest achievable fit for a given level of complexity considering all observations (MW-01 to MW-10). In that sense, the calibration and predictive errors shown in the first chart (i.e. the "1 zone model") are almost exclusively associated to the lack of complexity of the model and not to the chosen K value (i.e. there is no other K value that could lead to a better fit to the existing observations using only one K zone), meantime the errors of the last chart (i.e. the "36 zones model") are associated to an excess of complexity that leads to overfit in most observation wells.
Figure 5: Effect of model complexity on the predictive error for the MODFLOW/MT3DMS model.
Estimation of optimal complexity in groundwater models
A common approach used by data scientists for estimating the optimal complexity of a model is to separate the observations into two datasets: the training dataset, used to calibrate the model, and the testing dataset, used to verify that no under or overfitting is occurring. The associated methods are grouped under the name of cross-validation techniques, including the Train-Test split, the K-Fold CV and the Shuffle and Split. The use of cross-validation techniques is a fundamental step in the modelling process for data scientists, since as demonstrated before, minimum predictive error is only achieved if an optimal complexity is used. It is necessary to mention that cross-validation methods should be applied only when the existing observations are reasonably related to the predictions of interest, in terms of type, location, scales, and associated stresses.
We can see that cross-validation in data science is up to a certain point similar to an existing groundwater modelling approach, in which the historic period is split into a calibration and a validation period. That said, cross-validation techniques used by data scientists are fairly sophisticated algorithms, formulated with the specific objective of finding the optimal level of complexity of a model. Furthermore, the idea of separating the historic period into a calibration and a validation period is many times misinterpreted in groundwater modelling, to the point in which in many occasions the distinction is not even attempted because it is considered to be useless. This happens due to a misunderstanding of the underlying problem and available methods.
For the purpose of this article we apply a very simple version of the Train-Test split method to the MODFLOW/MT3DMS model, i.e. (1) we separate the observations into training (years 0 to 14) and testing (years 15 to 17) datasets, (2) we use the training dataset to calibrate the models associated to the different levels of complexity, and (3) we estimate the optimal complexity by finding the minimum RMS for the testing dataset (not for the training dataset, which always decreases with the number of K zones). The results are presented in Figure 6, which shows that the optimal complexity is approximately between six and twelve K zones, although other levels of complexity could have been evaluated for a more precise result.
Figure 6: Estimation of the optimal complexity using the Train-Test split method.
Summary
Finding the optimal level of complexity of a model is key for minimizing predictive error. Under and overfitting can deteriorate the predictive capacity of a model, especially if measurement errors are significant. Cross-validation methods from data science can be used to estimate the optimal complexity of groundwater models, when the existing observations are reasonably related to the predictive variables of interest, and when the amount and quality of the observations is adequate. That said, the use of these types of cross-validation methods is still uncommon in groundwater modelling, which means that there is not enough evidence to conclude about their real contribution in consulting projects considering all practicalities. Independent of this, it is important for groundwater modellers to understand the implications of under and overfitting, and the existing approaches for estimating the optimal level of complexity of a model.
Additional comments
Model complexity can have important practical implications for the development of a modelling project, which were not discussed in this article. Complex models can take an important amount of time to implement and run, potentially affecting the tasks that the modeller will be able to perform considering the available deadlines and budget. These factors need to be considered when estimating the optimal level of complexity of a model, ideally within a tier-based risk assessment framework.
The application of cross-validation techniques requires an important degree of automation, especially when using the most sophisticated types of cross-validation methods. GSMOD is in the process of incorporating cross-validation techniques commonly used by data scientists as part of its modelling workflow. These methods will be embedded within the Bayesian uncertainty analysis framework currently offered by GSMOD.
When using PEST and Pilot Points, modellers have additional tools that allow them to control the "complexity" of the model without having to change the number of Pilot Points. One of these tools is Tikhonov regularisation. Visit the
PEST homepage for additional information.